Fibonacci numbers

The existence of physical limits to the magnitude of numbers should not detract us from trying to solve yet another problem: computing Fibonacci numbers (see the paragraph on loops). We again consult mathematics on the lookout for a suitable recurrence relationship:

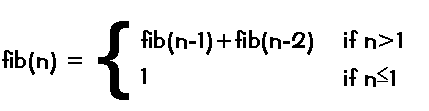
which we can readily transform into a Pico function:

Inspecting the function fib we might conclude that a lot of superfluous work is going on. For instance: fib(5) calls upon the computation of fib(4) and fib(3) and fib(4) calls upon the computation of fib(3) and fib(2) therefore fib(3) is computed twice! Actually, every function application of fib to a number greater than 1 generates two new applications. This indicates a kind of chain reaction where every recursive step doubles the number of computations.

This behaviour is confirmed by an experiment:

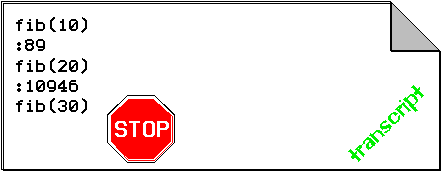
We actually have to pull the plug on the evaluator after 10 minutes have passed by without any result.

This illustrates the difference between the approach involving a recurrence relationship and our approach involving a Pico program. While mathematics is concerned with definitions and properties, we also have to take the explicit behaviour of our computational process into account.

In order to construct a more appropriate program to compute Fibonacci numbers, we start by examining the computational process that goes on in our own head:

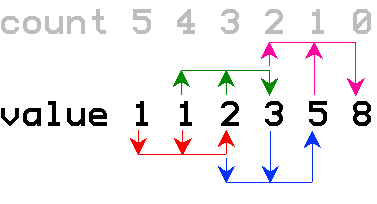
We start with the first two Fibonacci numbers and count steps while adding together two successive numbers to generate the following one. In contrast, our program performs the following action:

which is of course excessively cumbersome. Let us therefore try to adapt our program to our own way of dealing with this computation:

The new definition of the function fib is slightly more complicated than before: we have to provide parameters p and q to hold two successive Fibonacci numbers and a parameter r to hold a counter. We can easily identify the following progression of applications of fib:

indicating that the time consumed by our computational process is proportional to the index n of the required Fibonacci number. In our original program the time was proportional to 2ⁿ.