Let us consider a task to be performed using Pico: we want to establish a general function that is capable of computing the greatest common divisor (gcd for short) of two positive integers.
In order to solve this problem, we draw upon the following recurrence relationship from discrete mathematics:
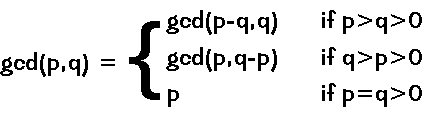
which states that the gcd of two distinct positive integers equal the gcd of the smallest and the difference between the greatest and the smallest. We can immediately transform this property into a computational process, using the combination of recursive function application and a selection:

The prescription of the function
gcd(x,y)
specifies that either gcd(xy,y),
gcd(x,y-x)
or x
is evaluated, depending on the relative values of
x
and y.
This is obtained through a careful application of two nested
references to the native if
function. Since at each recursive step, the values of the arguments
to gcd
become smaller and smaller, we will
eventually reach the gcd -which might be 1.